Generating Images with Desired Features

Generative Adversarial Networks (GANs) are the best choices of modern image synthesis, aren’t they? We already have hardly distinguishable face generator of StyleGAN2¹ (you can see an online demo) and this seems only a step away from the perfect image generation. However, even that SOTA model has limitations: how to generate an image with certain traits of interest? In other words, StyleGANs do not take any conditioning attributes on the resulting image but one long lengthy noise vector to generate an image. In this post, let’s take a look why this problem is hard and what are the efforts to solve (or at least, mitigate) it.

Why is generating a specific image by a GAN model hard?

In fact, if you want to generate an image of any cat with any species in any posture, then there’s no problem. You just can just train a GAN with a pile of cat image dataset. That’s not our interest at the moment. The thing is, how can we tell the model the length of the hair, or the orientation of the head and so on and on?

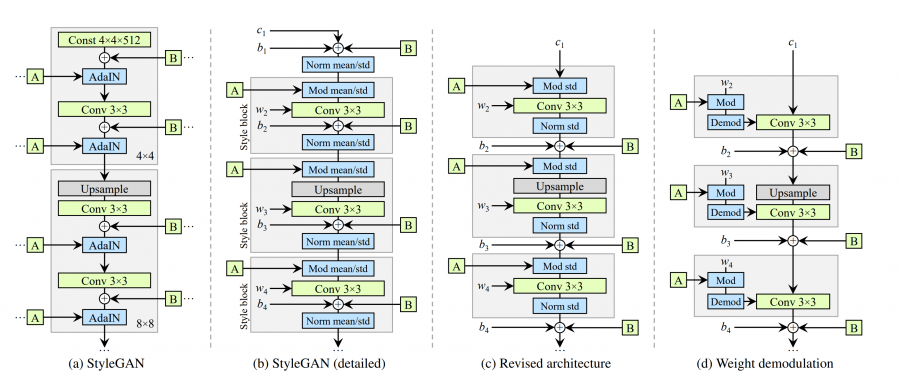
StyleGAN’s architectures. From the original paper¹.

As you can see on the above architecture, the StyleGAN family all get the input of A and B: A denotes the learned style vector and B stands for the broadcasted true noise. The difference between the architectures is out of the scope of this post, so let’s focus on what those input vectors mean.

No explicit mention of the feature

As you realised, there is no explicit part indicating which dimension means what feature of the resulting images. All the images are generated from the noise vectors and, in fact, it is nearly impossible to configure the image in advance to synthesis.

Entangled vector space

And yes, since the input vectors are noise, the model would not likely to learn the features correpond to a single dimension of the input. In other words, if we want to change the speices of cat, then we probably need to change several values on the input vector. Also the adjustment will be definitely non-linear, so there’s no chance to get Siamese by putting 1 to the 42nd value and Russian blue by 2. This chaotic situation is denoted as entanglement of the latent space.

In StyleGAN family, A is the mapped style vector from noise so it is in some way more disentangled, than the input noise space. It learns the ‘style’ from the noise and can be appliable to transfer the style to another generated image. Still, nonetheless, we don’t know which dimension stands for what.

Proposed methods

Facing those challenges, researchers are working on the interpretability of exiting models and novel architectures. Here I list up some of those works.

Feed the exact image to the model

Core algorithm of Image2StyleGAN. From the original paper².

Somehow unrealistic setting, isn’t it:) but if we can obtain the nice latent style vector producing the image we have, then we can play with the model much easier. Abdal et al.² proposed the simple gradient descent based algorithm for it.

This algorithm starts from a random vector and gradually optimise the style vector to produce as similar image as possible to the given image. Here, $L_{perceptual}$ is the perceptual loss (or perceptual distance) between two images. I mentioned briefly about this at my previous post. This perceptual loss is to minimise the stylistic difference between images by using pre-trained VGG-16 network’s interim results. Hence, the optimised latent style vector will produce the most similar image in terms of the pixels and the (machine) perception.

The authors already extended this to Image2StyleGAN++, but I would insist the powerful use case of this method regarding this post’s theme is that we can collect the style vectors from the set of images with our desired features. We could hopefully find some common directions from the vectors!

Provide details to the model

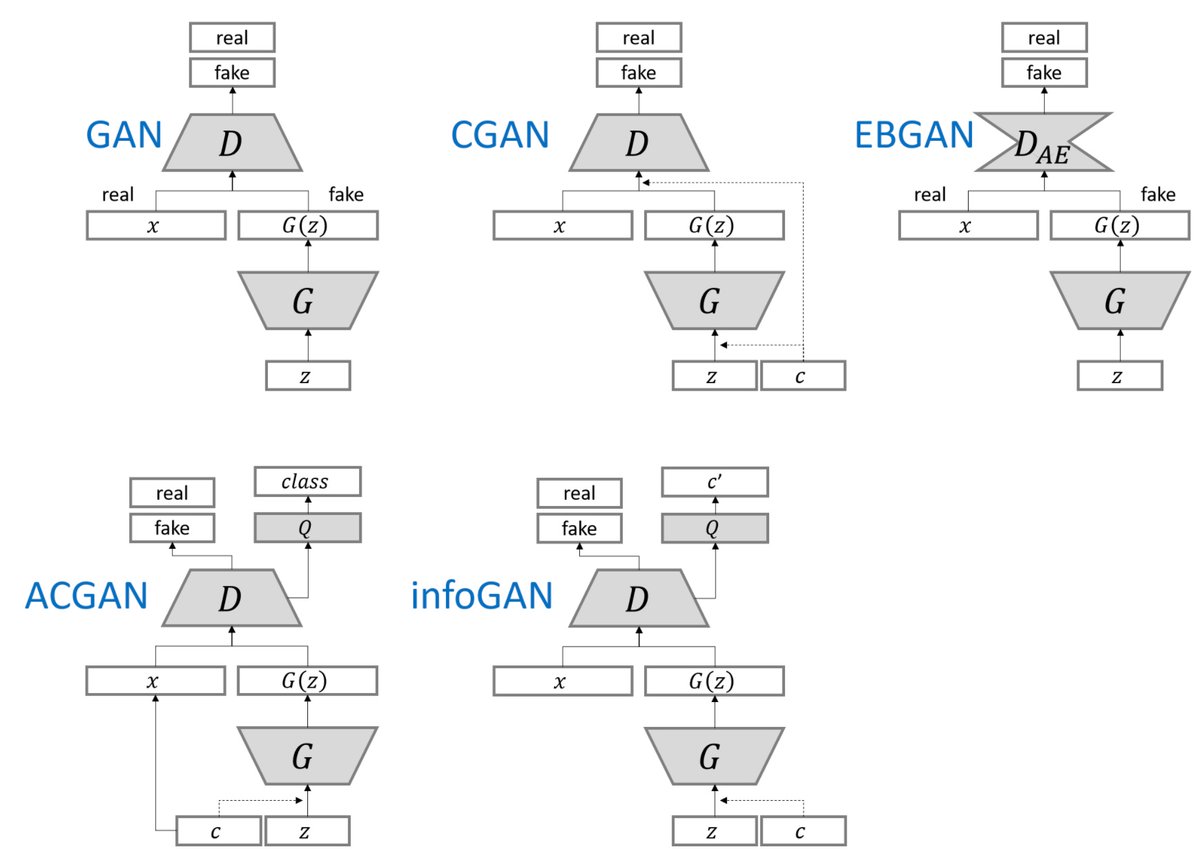
Some primitive GANs. Source unknown.

This is what ConditionalGAN³ tried at first - providing the additional input to the generator model. Early stage of works on GAN (image above) including CGAN, ACGAN and infoGAN shows how they tried to put the additional information to the entire architecture. This approach is intuitive as well as simple to implement. However, in many cases, those works are tested with categorical values at most 10 (and one or two continuous hidden features in infoGAN cases), so have limit on scalability.

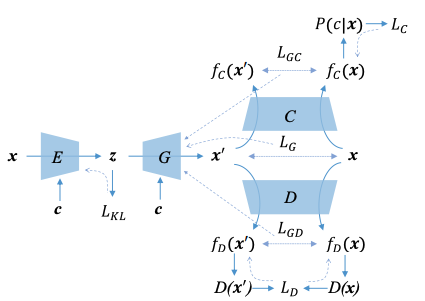
CVAE-GAN architecture and the loss propagation diagram. From the original paper⁴.

CVAE-GAN⁴ is an alternative to vanilla GAN approaches. You might heard about Variational Auto-Encoder, or VAE, to generate images just like GANs do but in deterministic way. The idea of VAEs is to encode the latent vectors from the real images and later decode them. In mathematical terms, the objective of VAEs is:

\[\log P(X) - D_{KL} [Q(z|X) \| P(z|X)] = \mathbb{E} [\log P(X|z)] - D_{KL} [Q(z|X) \| P(z)]\]

where $Q(z|x)$ is the encoder distribution. Simplifying the calculation, we usually model the true distribution $P$ with a Gaussian. Anyway, CVAE is just conditioning every term on the condition of interest, $c$.

VAE family usually performs ‘okay’ with blurry results, but at least in determinstic sense. CVAE-GAN merges two named architectures - treating the generator of GAN as the decoder of CVAE, and update them with the losses calculated from the auxiliary classifier and discriminator. To overcome the vanishing gradient during the GAN training, the authors proposed mean feature matching loss term as well, which is quite similar to the perceptual loss but within the model itself. Interested readers can read the original paper listed below.

Finding semantic transformations of the model

This is the post-processing approach of controlling GAN. In case of StyleGAN, after the image is generated, we can play with the style vectors to see which value corresponds to what visual feature. However, the style vector has 512 dimension by default setting and we may don’t have much time to play with each of the value. Plus, the style vector can still be entangled, so we might not find the exact feature we want by brute-force.

Yujun et al.⁵ proposed an elegant approach named SeFa (Semantic Factorization) to find significant transformations on several generative models, including StyleGAN v1 and v2, PGGAN, and BigGAN. Their idea is simple: take the first affine transformation of the generator and find the direction on the input vector which results in the most change in the objective space. Let’s formulate this by following authors’ logic.

Consider a generator $G$ taking an input $\mathbf{z} \in \mathbb{R}^d$. Denote $G_1$ be the first affine transformation of $G$. We can formulate this:

\[G_1(\mathbf{z}) = \mathbf{A} \mathbf{z} + \mathbf{b}\]

Let’s say the resulting dimension is $m$, so $\mathbf{A} \in \mathbb{R}^{m \times d}$ and $\mathbf{b} \in \mathbb{R}^m$. Editing the image can be denoted as:

\[G(\mathbf{z}') = G(\mathbf{z} + \alpha \mathbf{n})\]

where $\mathbf{n} \in \mathbb{R}^d$ is an unit vector and $\alpha$ is an manipulation intensity. From this preliminaries, let’s expand the first transformation with $\mathbf{z}’$.

\[\begin{align*} G_1(\mathbf{z}') &= G_1(\mathbf{z} + \alpha \mathbf{n}) \\ &= \mathbf{A} \mathbf{z} + \mathbf{b} + \alpha \mathbf{A} \mathbf{n} \\ &= G_1(\mathbf{z}) + \alpha \mathbf{A} \mathbf{n} \end{align*}\]

This states that the transformation is invariant to the bias trained. The authors propose to solve the following optimisation problem:

\[\mathbf{N}^* = \arg\max_{\mathbf{N} \in \mathbb{R}^{d \times k},\ \mathbf{n}_i^\intercal \mathbf{n}_i = 1,\ \forall i \in [k]} \Sigma_{i=1}^{k} \| \mathbf{A} \mathbf{n}_i \|_2^2\]

where $\mathbf{N} = [\mathbf{n}_1, \cdots, \mathbf{n}_k]$ and is the $k$-most-significant transformations. Introducing the Lagrange multipliers $\lambda_1, \cdots \lambda_k$ to solve:

\[\begin{align*} \mathbf{N}^* &= \arg\max \Sigma_{i=1}^{k} \| \mathbf{A} \mathbf{n}_i \|_2^2 - \Sigma_{i=1}^{k} \lambda_i (\mathbf{n}_i^\intercal \mathbf{n}_i - 1) \\ &= \arg\max \Sigma_{i=1}^{k} \left( \mathbf{n}_i^\intercal \mathbf{A}^\intercal \mathbf{A} \mathbf{n}_i - \lambda_i \mathbf{n}_i^\intercal \mathbf{n}_i - \lambda_i \right) \\ \frac{\partial}{\partial \mathbf{n}_i} \mathbf{N}^* &= 2 \mathbf{A}^\intercal \mathbf{A} \mathbf{n}_i - 2\lambda_i \mathbf{n}_i = 0 \end{align*}\]

so it searching $\mathbf{n}_i$ goes equivalent to finding $k$ eigenvectors with the largest eigenvalues of $\mathbf{A}^\intercal \mathbf{A}$. Simple, isn’t it? we can just add $\mathbf{n}_i$ with the scalar parameter $\alpha$ to adjust our image. Oh, this can make positive synergy with the first approach I introduced:)

Yes, I should admit that this approach may not lead to the features what we exactly want to find, but would insist this has much higher chance to find some meaningful transformations.

Wrap up

We went through the ways how to generate the image with our desired features. Nothing is so perfect - I’m still seeking and making experiments to control the image generation with as many attributes as possible. Until the mysteries of GANs be unveiled:)

Read more

1. Conditional Variational Autoencoder: Intuition and Implementation, A. Kristiadi, 2016
2. CVAE-GAN original paper, J. Bao et al., 2017
3. SeFa demo page